diff --git a/slides/bst.md b/slides/bst.md
new file mode 100644
index 0000000000000000000000000000000000000000..bdcd6a720801fef5986bf8a3018fc366609b3745
--- /dev/null
+++ b/slides/bst.md
@@ -0,0 +1,91 @@
+---
+title: Arbres de recherche binaires
+date: 2021-03-17
+---
+
+# Arbres binaires de recherche
+
+Qu'est-ce qu'un *arbre binaire de recherche* ou *binary search tree*?
+
+## Définition
+
+1. Arbre binaire: chaque nœud à **au plus** deux sommets enfants.
+2. Chaque nœud contient une clé.
+3. Pour chaque nœud, tous les nœud du **sous-arbre gauche** ont une clé
+ inférieure ou égale au nœud considéré et tous les nœuds du **sous-arbre
+ droit** du nœud considéré ont une clé supérieure ou égale au nœud considéré.
+
+La propriété 3 est connue sous le nom de propriété ABR (ou BST property).
+
+## Utilité
+
+* Recherche de clé, *min/max*.
+* File de priorité.
+* Parcours ordonné (parcours infixe) => tri.
+
+# Exemple
+
+## Un arbre binaire de recherche d'entiers
+
+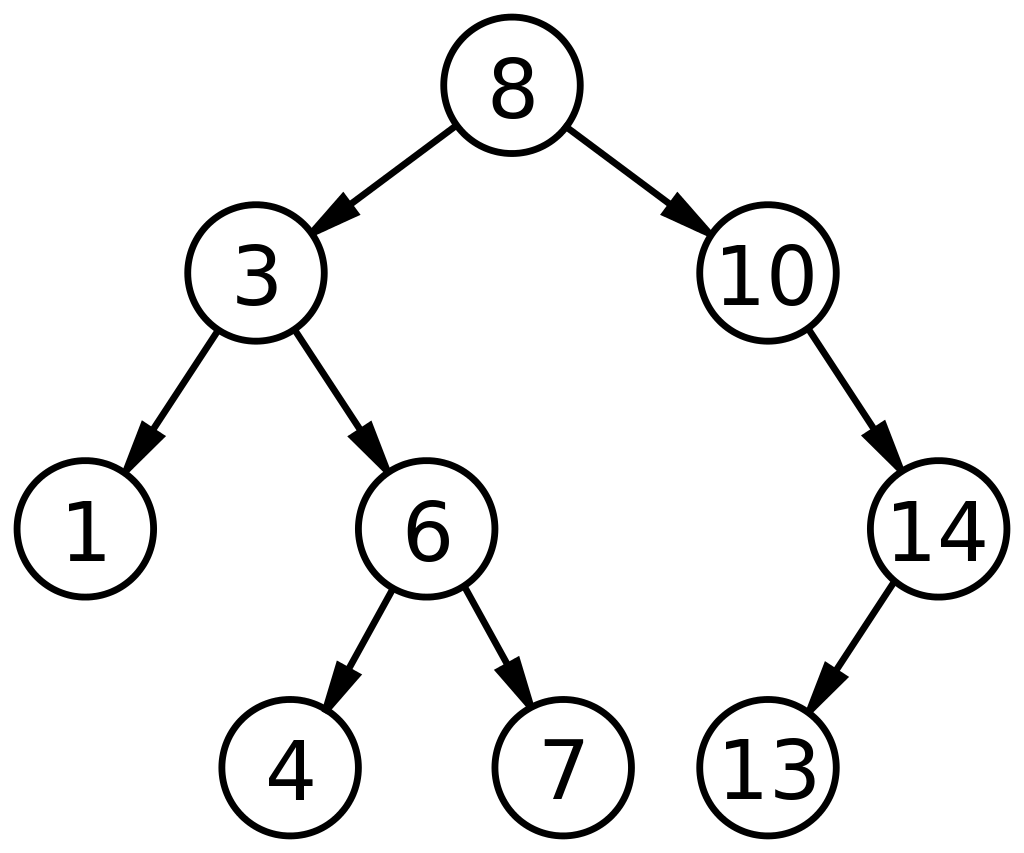{width=60%}
+
+# Structure de données
+
+## Fonctionnalités importantes
+
+\footnotesize
+
+1. Insertion de clé
+2. Recherche de clé
+3. Suppression de clé
+
+## Récursivité
+
+La propriété ABR est **récursive** (les sous-arbres doivent être ABR):
+
+ * L'enfant de gauche est plus petit que nœud courant?
+ * L'enfant de droite est plus petit que nœud courant?
+ * Le sous-arbre de gauche/droite est-il ABR?
+
+<!-- ```C -->
+<!-- bool is_bst(tree) { -->
+<!-- if (is_empty(tree)) return true; -->
+<!-- // l'enfant de gauche est plus grand => faux -->
+<!-- if (!is_empty(tree.left) && tree.left.key > tree.key) return false; -->
+<!-- // l'enfant de droite est plus petit => faux -->
+<!-- if (!is_empty(tree.right) && tree.right.key < tree.key) return false; -->
+<!-- // récursivement si les sous-arbres sont pas des ABR -->
+<!-- if (!is_bst(tree.left) || !is_bst(tree.right)) return false; -->
+<!-- } -->
+<!-- ``` -->
+
+# L'insertion
+
+\footnotesize
+
+Insertion récursive:
+
+```C
+tree insert(tree, key) {
+ // fin de la récursion, on crée le noeud et retourne
+ si l'arbre est vide:
+ return create_node(key);
+ // recherche d'où insérer
+ si la clé est plus petite que le noeud courant:
+ si le sous-arbre gauche est vide:
+ sous-arbre gauche = create_node(key);
+ sinon:
+ return insert(tree, key);
+ si la clé est plus grande que le noeud courant:
+ si le sous-arbre droit est vide:
+ sous-arbre droit = create_node(key);
+ sinon:
+ return insert(tree, key);
+ // on retourne l'arbre!
+ return tree;
+}
+```
+
+
+