More docs
Showing
- src/figs/amdahls-law.png 0 additions, 0 deletionssrc/figs/amdahls-law.png
- src/figs/communication_1d.png 0 additions, 0 deletionssrc/figs/communication_1d.png
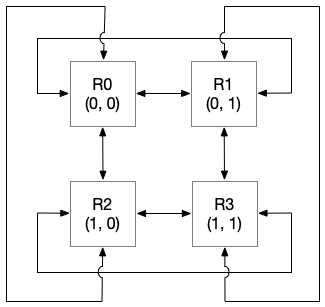
- src/figs/communication_2d.png 0 additions, 0 deletionssrc/figs/communication_2d.png
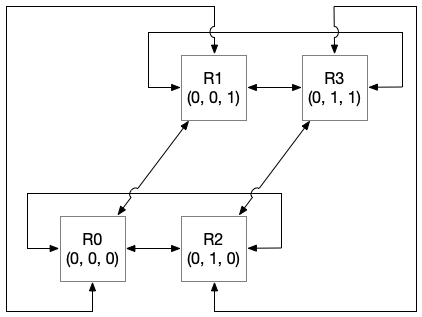
- src/figs/communication_3d.png 0 additions, 0 deletionssrc/figs/communication_3d.png
- src/figs/front-logo.png 0 additions, 0 deletionssrc/figs/front-logo.png
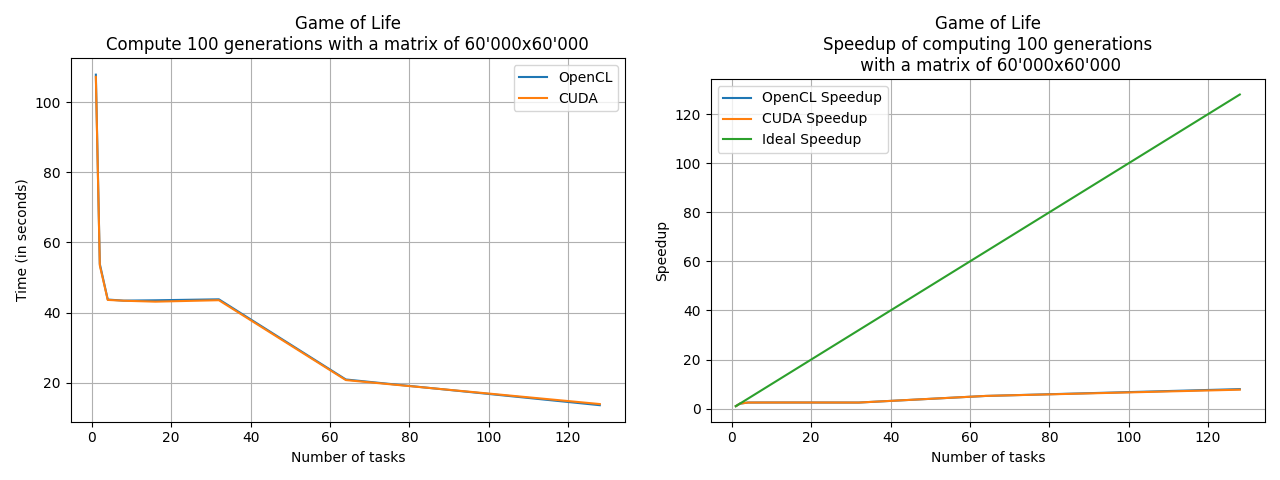
- src/figs/gol_result_and_speedup_gpu.png 0 additions, 0 deletionssrc/figs/gol_result_and_speedup_gpu.png
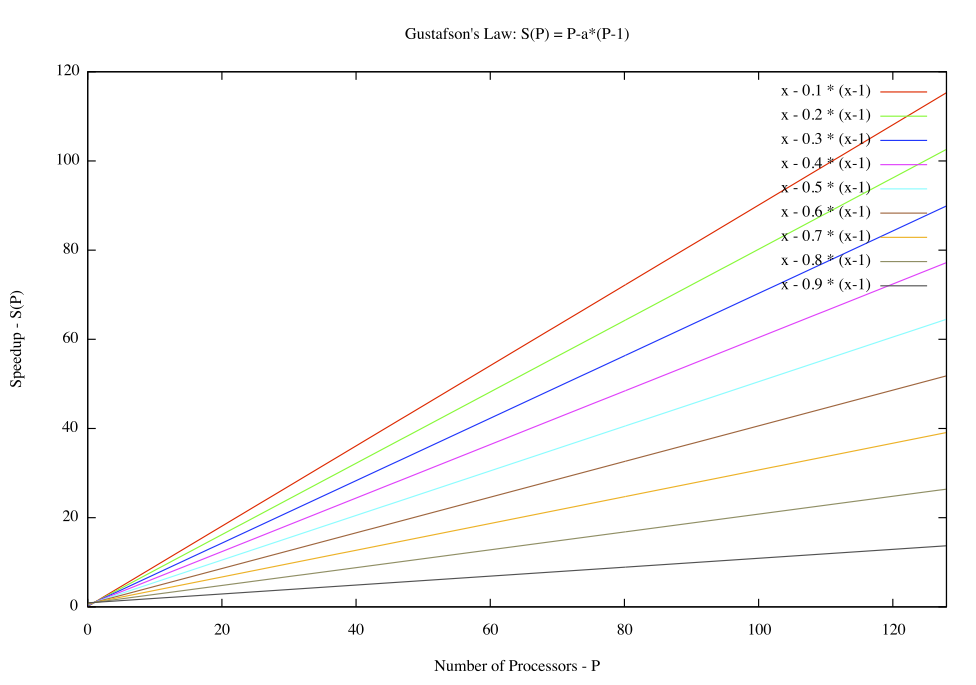
- src/figs/gustafson-law.png 0 additions, 0 deletionssrc/figs/gustafson-law.png
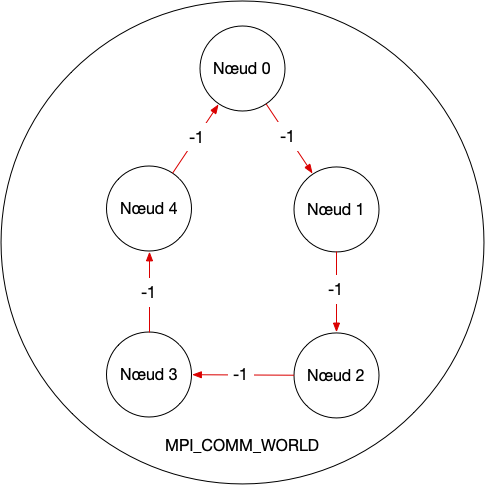
- src/figs/ring.png 0 additions, 0 deletionssrc/figs/ring.png
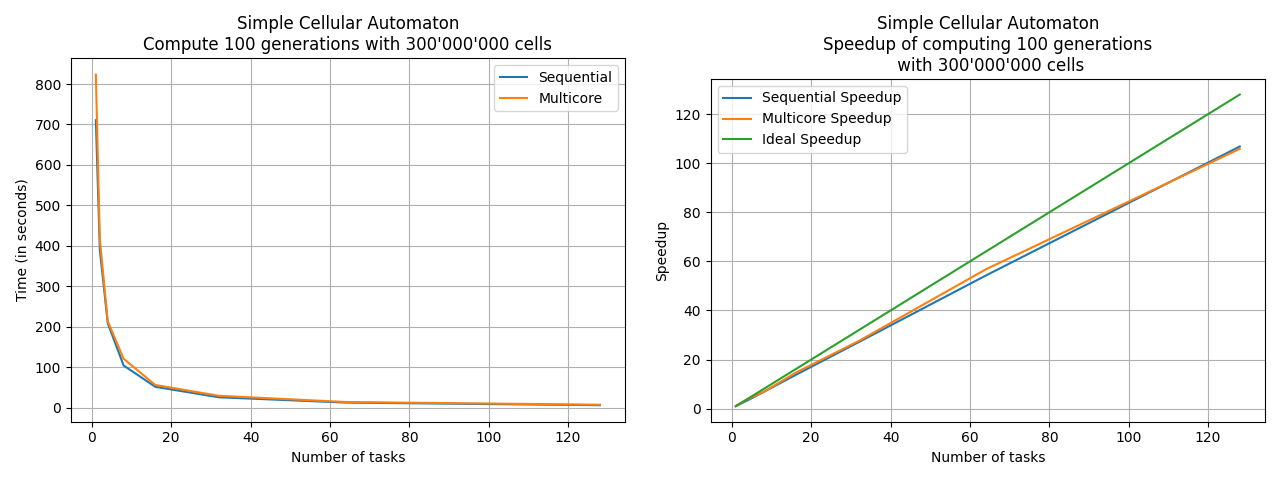
- src/figs/sca_result_and_speedup.png 0 additions, 0 deletionssrc/figs/sca_result_and_speedup.png
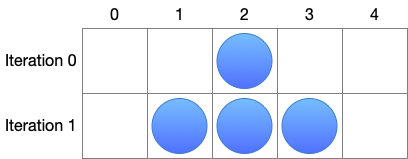
- src/figs/simple_automate.png 0 additions, 0 deletionssrc/figs/simple_automate.png
- src/text/00-preface.md 4 additions, 4 deletionssrc/text/00-preface.md
- src/text/02-introduction.md 9 additions, 4 deletionssrc/text/02-introduction.md
- src/text/03-programmation-parallele.md 3 additions, 0 deletionssrc/text/03-programmation-parallele.md
- src/text/04-mpi.md 12 additions, 24 deletionssrc/text/04-mpi.md
- src/text/04-programmation-parallele.md 0 additions, 42 deletionssrc/text/04-programmation-parallele.md
- src/text/05-futhark.md 15 additions, 11 deletionssrc/text/05-futhark.md
- src/text/06-mpi-x-futhark.md 60 additions, 0 deletionssrc/text/06-mpi-x-futhark.md
- src/text/07-automate-elementaire.md 114 additions, 0 deletionssrc/text/07-automate-elementaire.md
- src/text/07-jeu-de-la-vie.md 0 additions, 35 deletionssrc/text/07-jeu-de-la-vie.md
- src/text/08-jeu-de-la-vie.md 166 additions, 0 deletionssrc/text/08-jeu-de-la-vie.md
src/figs/amdahls-law.png
deleted
100644 → 0
35.8 KiB
src/figs/communication_1d.png
0 → 100644
5.41 KiB
src/figs/communication_2d.png
0 → 100644
10.9 KiB
src/figs/communication_3d.png
0 → 100644
13 KiB
src/figs/front-logo.png
0 → 100644
2.47 KiB
src/figs/gol_result_and_speedup_gpu.png
0 → 100644
67 KiB
src/figs/gustafson-law.png
deleted
100644 → 0
93 KiB
src/figs/ring.png
0 → 100644
34.9 KiB
src/figs/sca_result_and_speedup.png
0 → 100644
79.4 KiB
src/figs/simple_automate.png
0 → 100644
12 KiB
src/text/03-programmation-parallele.md
0 → 100644
src/text/06-mpi-x-futhark.md
0 → 100644
src/text/07-automate-elementaire.md
0 → 100644
src/text/07-jeu-de-la-vie.md
deleted
100644 → 0
src/text/08-jeu-de-la-vie.md
0 → 100644