01_analyse_dimensionnelle.md



Avertissement {#avertissement .unnumbered}
Cette tentative de polycopié contient certainement un grand nombre
d'erreurs étant donné qu'elle est développée en même temps que le cours
est donné et qu'elle en est à ses premiers mois de vie. Quand vous
trouverez des erreurs n'hésitez pas à me les communiquer et ainsi
améliorer la qualité de ce polycopié. Toute erreur trouvée concernant de
la "physique" (pas les fautes d'orthographe donc) seront récompensées
par un bonus sur la note des contrôles continus.

Bibliographie {#bibliographie .unnumbered}
Il existe une multitude de bons livres de physique générale à
disposition. Ce polycopié est largement inspiré du livre de D. C.
Giancoli, Physics: principles with applications, 7-th edition,
Pearson, 2014. D'autres lectures possibles sont les suivantes:


Walker, Halliday & Resnick, Fundamentals of Physics, Wiley, 2014.


E. Hecht, Physique, 1999.


Une partie de la bibliographie que je vous ai donné est en anglais. Il
existe des traductions qui sont en principe disponibles à la
bibliothèque.

Analyse dimensionnelle

Généralités
Toues les sciences "naturelles" sont basées sur l'observation du monde
qui nous entoure. Mais malgré le fait qu'on ait l'impression que le
processus d'observation soit une suite simple: observation,
expérimentation, obtention de résultats, qu'on explique avec une
théorie (un ensemble de lois) cela n'est pas vraiment le cas. En
fait, de façon proche à ce qui se passe dans les arts, les sciences sont
un processus hautement créatif. En effet, lors d'une observation un
scientifique ne décrit pas tout ce qu'il voit, mais sélectionne
uniquement ce qu'il juge important pour la compréhension et
l'interprétation d'un phénomène. De plus, une fois sélectionné le
processus à observer, il convient de créer une expérience permettant de
le mesurer de façon aussi précise que possible pour pouvoir le décrire.
La mesure tient donc une place centrale dans les sciences et se complète
parfaitement avec la création de théories qui permettent l'explication
d'observations. Par ailleurs, toutes les théories ne sont pas le fruit
d'expériences (ou d'observations) mais ont souvent été le résultat de
constructions de l'esprit. Dans ce cas les expériences, viennent
confirmer (ou infirmer) les théories. En effet, une théorie physique est
supposée vraie jusqu'à ce qu'une expérience vienne l'infirmer (on ne
peut pas prouver une théorie).
Les expériences ont donc deux fonctions principales

Collecter des données qui permettront la dérivation de lois physiques.
Vérifier ou infirmer les lois physiques.

Les lois physiques sont des outils très pratiques permettant la
prédiction quantitative de phénomènes (et non la "post-diction" comme
avec les expériences). Il est par exemple possible de prédire très
précisément la hauteur à laquelle il faut lancer un satellite pour qu'il
se retrouve en orbite géostationnaire (et donc connaître la quantité de
carburant nécessaire par exemple) grâce aux lois de Newton. Ce qui
serait certainement beaucoup plus difficile à déterminer
expérimentalement, s'il fallait faire des dizaines d'essais jusqu'à ce
que ça marche.
Par ailleurs, beaucoup de "lois" ont des capacités prédictives mais ne
sont pas complètement générales. Par exemple, bien que les lois de
Newton marchent très très bien pour notre vie de tous les jours,
certaines applications d'usage quotidien ne fonctionneraient pas si on
s'en tenait là. En effet, le GPS requiert l'extension des lois de Newton
à la relativité générale pour pouvoir fonctionner correctement. En fait
la gravitation Newtonienne est une approximation de la relativité
générale.
Ces approximations sont souvent le résultat de simplifications faites
dans la représentation dont ont se fait de processus physiques: les
modèles. Un modèle est une vision de l'esprit qui permet de réunir
plusieurs situations qui à première vue peuvent paraître non-semblables
ou à simplifier un problème afin de pouvoir le résoudre plus simplement.
Par exemple un liquide est composé d'atomes qui se déplacent. Il serait
possible (mais complètement infaisable et inutile dans presque tous les
cas) d'étudier chaque atome individuellement pour avoir une description
très détaillée du mouvement d'un fluide. Néanmoins, il est beaucoup plus
simple de faire l'hypothèse qu'un fluide peut être considéré comme un
objet continu.
Les modèles permettent également un traduction en équations mathématiques
d'un phénomène naturel. Ces équations peuvent ensuite d'être résolues
à la main ou  par ordinateur, chose que nous ferons durant ce cours.
Mais avant d'aller plus loin, nous allons discuter des dimensions des différentes grandeurs
physiques et leurs dimensions.

Unités, Système International
Toute mesure doit être effectuée par rapport à un "standard" ou unités.
Cela n'a aucun sens de dire qu'un éléphant pèse 36, si nous ne disons
pas 36 en quelles unités. Pour chaque grandeur de multiple standards ont
été créé au cours des années qui sont devenus de plus en plus précis
avec les avancées technologiques (combien exactement mesure
 $1{\mathrm{m}}$ , la durée d'une seconde, etc). Dans cette section nous
allons discuter les unités des grandeurs de base de la physique. Nous
verrons en particulier le Système International (ou SI).
Ne pas se mettre d'accord sur un système d'unités peut avoir des
conséquences catastrophiques. Un exemple récent est la perte du
satellite Mars Climate Orbiter (le coût de la mission était de 330
millions de dollars) qui a explosé alors qu'il essayait de se mettre en
orbite autour de Mars, car une partie du code informatique récoltant les
donnée de la sonde donnait des résultats en unités non-SI alors que la
NASA travaillait en SI. Il y a donc eu une très grossière erreur dans le
calcul de la trajectoire à adopter pour la mise en orbite et le
satellite s'est écrasé (plus de détails ici par exemple
https://fr.wikipedia.org/wiki/Mars_Climate_Orbiter).
Les unités sont définies par rapport à des grandeurs "facilement"
mesurables avec une grade précision et qui ne changent pas (ou très très
très peu) au cours du temps.

Longueur
Le standard international fût établi par la France dans les années 1790.
Pour les unités de longueur est le mètre (abrégé 
 ${\mathrm{m}}$ ). A
l'origine le mètre était 1/10'000'000 de la distance entre l'équateur et
un des pôles. A partir de cette mesure un étalon en platine fût forgé
(c'est quand même plus pratique à utiliser). Puis, en 1889, le mètre a
été défini comme la distance entre deux très fines encoche sur une barre
d'un alliage platine-iridium. Comme cette façon de définir le mètre
n'était pas suffisamment précise pour beaucoup d'applications, en 1960
le mètre devint  $1'650'763.73$  longueur d'onde d'une lumière émise par
le gaz krypton-86. En 1983, fût redéfini comme la distance parcourue par
la lumière en 1/299'792'458 secondes.
Il existe d'autres unités de longueur, par exemple les britanniques
utilisent le pouce ou inch (1
 $\mathrm{in.}$  correspond à
0.0254 ${\mathrm{m}}$ ). Dans ce cours nous nous concentrerons
principalement sur le système SI.
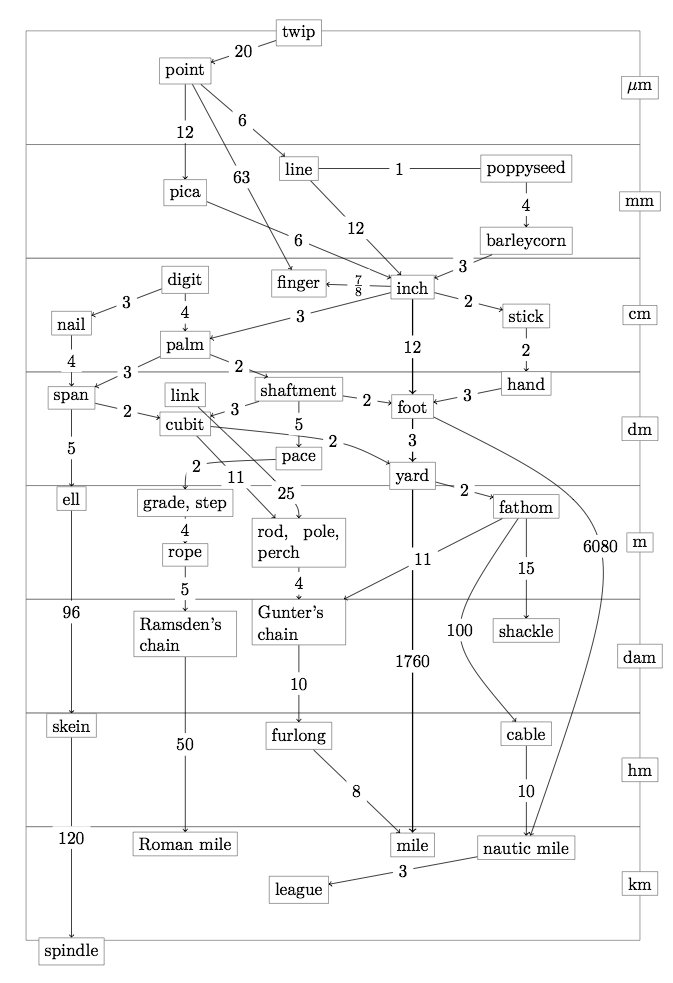
A titre de comparaison la @fig:imperial montre les relations entre les
différentes unités de longueur qui existaient dans l'empire britannique.
On y voit un très grand nombre d'unités différentes reliées entre elles par des relations
plus ou moins compliquées. La page wikipedia
https://fr.wikipedia.org/wiki/Unit%C3%A9s_de_mesure_anglo-saxonnes contient les unités anglosaxonnes
pour des surfaces et des volumes également.


Temps
La mesure du temps en SI est donnée en secondes (abrégée
 ${\mathrm{s}}$ ). Une seconde a longtemps été définie comme étant
 $1/(3600\cdot 24)=1/86'000$ -ème de journée solaire. La vitesse de
rotation de la terre se ralentissant légèrement d'année en année, il a
été nécessaire de raffiner de plus en plus cette définition. A présent
une seconde correspond à un processus atomique. Il s'agit du temps
nécessaire à 9'192'631'770 de la transitions entre deux états de l'atome
de césium 133.

Masse
Le kilogramme (abrégé 
 ${\mathrm{kg}}$ ) est la masse d'un étalon
international du kilogramme. En 1795, le kilogramme était la d'un
décimètre cube d'eau à une température de  $4^\circ{\mathrm{C}}$ . Puis il
a été remplacé par un étalon en platine iridié (voir Fig. {@fig:kg}).
Il s'agit de la seule unité utilisant encore un étalon, aucune "grandeur
naturelle" n'ayant pu être utilisée pour définir le kilogramme
autrement. Des copies de cet étalon ont été fabriquée et envoyées à
chaque état qui en ont fait d'autres copies officielles pour contrôler
les balances utilisées un peu partout sur les territoires.


Température
La température mesure le degré d'échauffement d'un corps. En SI l'unité
de la température est le degré Kelvin (abrégé 
 ${\mathrm{K}}$ ). Il est
défini comme le  $1/273.16$ -ème de la température du point triple de
l'eau (la température où les trois phases, solides, liquides, gazeuse,
de l'eau peuvent coexister en équilibre thermodynamique). Cette
température se trouve par définition à  $273.16^\circ{\mathrm{K}}$  ou
encore à  $0.01^\circ{\mathrm{C}}$ . Nous verrons un peu plus de détails
sur la définition du zéro degrés Kelvin (ou zéro absolu) dans la suite
du cours.

Courant
L'intensité du courant électrique est mesurée en Ampères (abrégé
 ${\mathrm{A}}$ ). Le courant est la quantité de charge par seconde
qui passe dans un élément conducteur. On définit un ampère de façon
un peu complexe. C'est l'intensité de courant constant qui
circulerait dans deux fils conducteurs infinis placés dans le vide, de
section négligeable, et placés à une distance d'un mètre l'un de l'autre
qui produirait une force de  $2\cdot 10^{-7}$  Newton par longueur de
mètre. Les autres unités très utiles en électricité, l'ohm (abrégé
 $\Omega$ 
) et le volt (abrégé  ${\mathrm{V}}$ ) se déduisent ensuite par
les fameuse formules  $U=R\cdot I$ 
( $[{\mathrm{V}}]=[\Omega]\cdot [{\mathrm{A}}]$ 
) et  $P=U\cdot I$ 
( $[{\mathrm{W}}]=[{\mathrm{V}}]\cdot [{\mathrm{A}}]$ 
).
Avec ces relations, on constate qu'on peut déduire les unités
de la résistance et de la tension en fonction de toutes celles que
nous avons déjà vues précédemment.

Ordre de grandeur
Souvent nous pouvons vouloir qu'une estimation rapide d'une quantité ou
simplement vouloir rapidement avoir une idée de comment "marche" un
processus. Pour ce faire plutôt que d'entrer complètement dans tous les
détails compliqués des calculs il peut être beaucoup plus simple de
fonctionner avec des ordres de grandeurs de nos quantité (en gros on
arrondit tout à l'entier ou même à la puissance de 10)[^1]. On a donc un
résultat précis "à la puissance de 10 près".

Exercice (Volume d'un lac) #
Calculez le volume du lac Léman sachant qu'il fait environ
 $70{\mathrm{km}}$ 
 de long pour  $10{\mathrm{km}}$  de large et
 $100{\mathrm{m}}$ 
 de profondeur.[^2]


Exercice (Hauteur d'un bâtiment) #
Je souhaite estimer la hauteur d'un bâtiment. Supposons que mes yeux
soient à une hauteur de 
 $1.5{\mathrm{m}}$  du sol. La seule information
connue est que quand je me place à une distance d'un écartement de bras
d'un arbre (mesurant environ  $3{\mathrm{m}}$  de haut et se trouvant à
 $20$  pas du bâtiment) placé entre moi et le bâtiment, l'arbre cache tout
juste le haut du bâtiment.


Exercice (Épaisseur d'une feuille de papier) #
Vous avez à disposition une règle (précise au millimètre) et un livre.
Estimez aussi précisément que possible et avec un minimum d'effort
l'épaisseur d'une feuille du livre.


Analyse dimensionnelle
Lorsque nous parlons de dimensions d'une quantité, nous nous référons
souvent au type des unités de la quantité. Une longueur sera représentée
par 
 $[L]$ 
[^3], un temps par  $[T]$ 
, une masse par  $[M]$ , etc. Cette
notation se généralise pour toute quantité dont les quantités sont des
combinaisons (multiplication ou division) de ces unités de base. Ainsi,
une surface sera  $[L^2]$ 
, une fréquence  $[1/T]$ 
, une vitesse  $[L/T]$ ,
une énergie  $[M\cdot L^2/T^2]$ 
, une force  $[M L/T^2]$ 
, etc.

Exercice (Quantité de grandeur de base) #
Écrivez les 5 types d'unités fondamentales nécessaires à la dérivation
de toutes les autres.

L'analyse dimensionnelle peut se révéler particulièrement utile pour
vérifier si des relations font du sens ou pas. Les lois physiques
mettent en relation différentes quantités qui doivent être consistante
également du point de vue des unités. On ne peut naturellement pas
additionner des quantités qui n'ont pas les mêmes unités. Cela
reviendrait à ajouter des éléphants à des lettres, le résultat serait
alors peu clair.
Si nous prenons comme exemple la relation
 $s=x_0+\frac{1}{2}v_0 t^2,$ 
qui décrirait la position d'un objet en mouvement rectiligne uniforme,
 $s$ 
, qui partirait d'une position  $x_0$ 
, aurait une vitesse  $v_0$  après
un temps  $t$ . Si nous effectuons l'analyse dimensionnelle de cette
relation nous avons
 $\begin{aligned} [L]&\stackrel{?}{=}[L]+[L/T]\cdot [T^2],\nonumber\\ &\neq[L]+[L\cdot T]. \end{aligned}$ 
On constate donc que cette équation
est certainement fausse. On note aussi que le  $1/2$  n'ayant pas d'unités
a été simplement ignoré dans la relation ci-dessus, car il n'est pas
porteur d'unités.
Si le résultat de l'analyse dimensionnelle se révèle incohérent, nous
sommes certains que l'équation est fausse. L'inverse est cependant faux.
En effet, une analyse dimensionnelle d'une équation cohérente ne permet
pas d'être sûr que l'équation en elle-même est correcte. Par exemple
tous les facteurs numériques peuvent être complètement faux. Ou alors
certaines quantités peuvent avoir les bonnes unités mais n'avoir aucun
sens physique dans les cas étudiés.

Exercice (Analyse dimensionnelle) #
Essayez de deviner les relations entre les quantités suivantes à partir
de leurs dimensions

Distance et vitesse.
Accélération et vitesse.
Distance et accélération.
Énergie et vitesse.
Force et énergie.
Énergie et tension.